13-From Randomness to Probability

13.1 Random Phenomena¶

1，

随机现象random phenomenon：	我们知道可能会发生什么结果，但我们不知道会发生什么特定的结果。
trial试验：	In general, each occasion upon which we observe a random phenomenon is called a trial.
结果outcome：	At each trial,the value of the random phenomenon,
事件event：	When we combine outcomes like that, the resulting combination is an event.
样本空间：	We call the collection of all possible outcomes the sample space.用S来表示事件
empirical probability	Because this definition is based on repeatedly observing the event’s outcome, this definition of probability is often called empirical probability.
	A phenomenon consists of trials. Each trial has an outcome. Outcomes combine to make events. For a random phenomenon, the sample space, S, is the set of all possible outcomes of each trial.

2，The Law of Large Numbers

2.1 大数定律(LLN)的原则说，当我们反复重复随机过程时，事件发生的比例确实降到一个数字。我们把这个数字称为事件的概率。【the probability of the event.】要满足两个条件

1）每一个trial发生的概率必须一样，

2）而且independent【 doesn’t affect the outcomes of the others】 3，不存在平均定律The Nonexistent Law of Averages 所谓的平均法根本不存在。但你会听到人们谈论它。一个优秀的击球手是在过去的六次三振吗？如果你在每周的统计学小测验中做得特别好，你的成绩不好吗？No.这不是随机现象的工作方式。没有短期内的平均收益法。

案例

13.2 Modeling Probability¶

1，概念 | theoretical probability. | 当概率来自一个数学模型而不是来自观察时，它被称为理论概率。 | |--------------------------|------------------------------------------------------------|

2，运算公式

注意：我们经常使用大写字母，通常从字母表的开始，来表示事件。我们总是使用P来表示概率正式时，使用小数（或分数）表示概率值，但有时，特别是更非正式交谈时，更容易使用百分比。

不要陷入认为随机事件总是同样可能的境地。赢得彩票的机会很小，尤其是那些回报很大的彩票

3，Personal Probability 3.1 subjective or personal probability：你对你获得A的机会的个人评估表达了你对结果的不确定性。这种不确定性可能是基于你在课程中的舒适度或中期成绩，但它不能基于长期的行为。我们称这第三种概率称为==主观概率或个人概率==。虽然个人概率可能基于经验，但它们既不是基于长期的相对频率或同样可能发生的事件。所以它们不会显示出我们所需要的一致性。因此，我们将坚持正式定义的概率。你应该注意到这个区别。

个人概率和其他两种概率之间的界限可以是模糊的。当天气预报员预测40%的降雨概率时，这是个人概率还是相对频率概率？他们声称可能是40%的时间，当地图看起来是这样的时候，它已经下雨了（经过一段时间）。或者预测员可能在陈述一种基于多年经验的个人观点，反映了对过去在类似情况下发生的事情的感觉。当你听到一个概率陈述，试着确定什么样的概率是意图。

4，The First Three Rules for Working with Probability 1. Make a picture. 2. Make a picture. 3. Make a picture.

13.3 Formal Probability¶

规则1：如果概率为0，事件永远不会发生，同样，如果概率为1，它总是发生。即使您认为一个事件非常不太可能，它的概率也不可能是负的，而且即使您确定它将会发生，其概率也不能大于1。（考虑一下相对的频率。）所以我们需要那个要求

规则·2：规则3：假设你按时上课的概率是0.8。你不能按时去上课的可能性是多少？是的，它是0.2。不是A的结果集称为A的补体，表示AC。这就导致了补充规则：

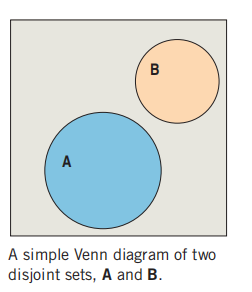
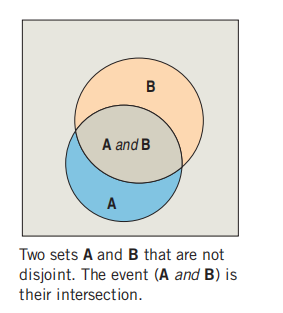
规则4： Disjoint (or mutually exclusive) events have no outcomes in common.

概率分配规则告诉我们，要成为概率的合法分配，所有可能结果的概率的总和必须完全是1。不再，同样少。

规则5：独立性意味着一个事件的结果不会影响另一个事件的结果。 indepen dence means that the outcome of one event doesn’t influence the outcome of the other.

案例

注意，“至少”通常是考虑补充的提示。至少会发生一次的事情。至少发生一次是根本不发生的补充，而且这更容易找到。至少发生一次--》至多发生0次 Some = At Least One

特别注意：注意那些不超过1的可能性。如果事件并非不一致，则不要添加这些事件的可能性 ==如果事件不独立，则不要乘以其概率。== Don’t confuse disjoint and independent

小结