16-Probability Models
你要抽小卡，已知20%的盒子里有一张希望独奏的照片，30%的盒子是丹尼卡·帕特里克的照片，其余的是布莱克·格里芬的照片。
16.1 Bernoulli Trials¶
假设你是唯粉，你只关系抽到本命，抽到本命的卡的概率0.2 每一次开卡的行为称为一次trail
■ There are only two possible outcomes (called success and failure) on each trial. Either you get Hope’s picture (success), or you don’t (failure). ■ The probability of success, denoted p, is the same on every trial. Here p = 0.20. ■ The trials are independent. |
|---|
Situations like this occur often and are called Bernoulli trials.
伯努利试验（Bernoulli experiment）是在同样的条件下重复地、相互独立地进行的一种随机试验， 其特点是该随机试验只有两种可能结果：发生或者不发生。 我们假设该项试验独立重复地进行了n次，那么就称这一系列重复独立的随机试验为n重伯努利试验，或称为伯努利概型。 单个伯努利试验是没有多大意义的，然而，当我们反复进行伯努利试验，去观察这些试验有多少是成功的，多少是失败的，事情就变得有意义了，这些累计记录包含了很多潜在的非常有用的信息 |
|---|
Let’s call this random variable Y = # boxes and build a probability model for it
| 抽一次中，抽两次中，抽第五次才中的概率： |  |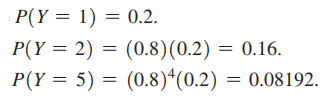
|---|
16.2 The Geometric Model¶
作用：模拟在一系列伯努利试验中取得第一次成功的概率
1，几何模型完全由一个==参数p、成功的概率==指定，并表示GEOM(p)。由于在试验编号x上取得第一次成功需要第一次经历x-1失败，所以概率很容易用一个公式来表示。
案例
2，Independence
伯努利试验的一个重要要求是这些试验是独立的。
10%的条件：伯努利试验必须独立的。如果违反了这个假设，只要样本小于10人口的%，仍然可以继续进行
案例
16.3 The Binomial Model¶
1，作用：求在n实验中几次成功的概率
案例
案例
16.4 Approximating the Binomial with a Normal Model¶
1，Binom(50, 0.2),
案例
*16.5 The Continuity Correction¶
16.6 The Poisson Model¶
1，泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布：计算一段时间内发生x次的概率 指数分布：是描述泊松过程中的事件之间的时间的概率分布【下一次发生的概率】 |
|---|
2，什么时候用合适呢
16.7 Other Continuous Random Variables: The Uniform and the Exponential¶
一、The Uniform Distribution¶
1，对于连续均匀性，我们希望所有相同长度的时间间隔都具有相同的概率
2，案例
例如，假设您到达一个公交车站，并想要模拟您等待下一辆公交车的时间。标志上写着公交车大约每20分钟就到一次，但没有提供其他信息。你可能会假设到达同样可能是在未来20分钟内的任何地方，所以概率模型将是
二、The Exponential Model¶
指数模型用于泊松模型计算时间段的时候
1，我们已经看到，泊松模型是事件的到达或发生的一个很好的模型。例如，假设我们使用泊松来建模x在下一分钟内访问我们的网站的概率。然后，可以使用参数为l的指数模型来模拟这些事件之间的时间。因为时间是一个连续的量，所以它有一个连续的模型，它的形式为：
总结
补充
Continuous random variable
