6-sorting

Part A-search

Part B-sorting Comparison based sort

1，Bubble Sort 思路

	

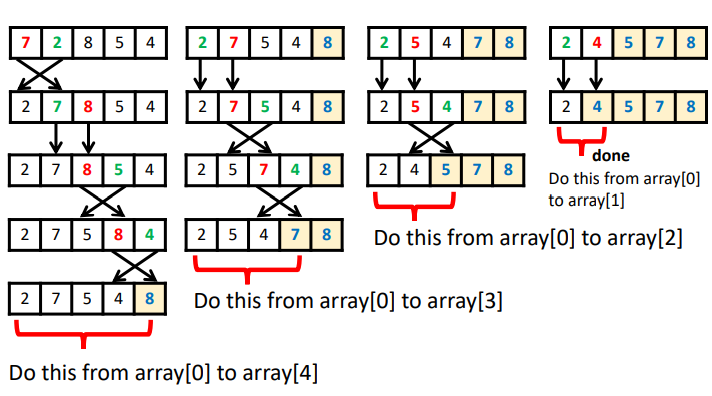代码 public static void bubbleSort(int arr[]) { for(int i=0;i<arr.length-1;i++) { for(int j=0;j<arr.length-1-i;j++) { if(arr[j]>arr[j+1]) { int temp=arr[j]; arr[j]=arr[j+1]; arr[j+1]=temp; } } } }

2，selection sort 一直把最小的放在前面

	

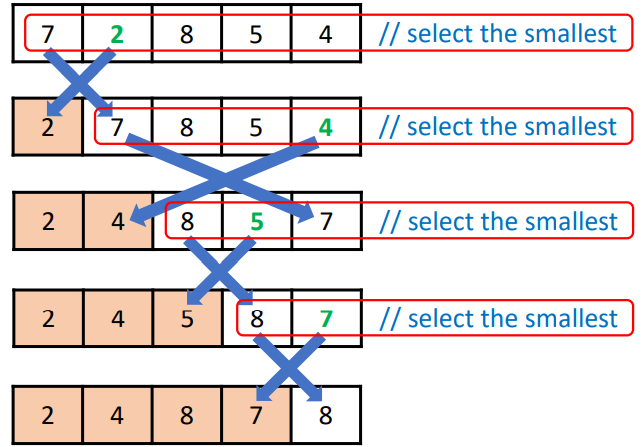3，insertion sort

	

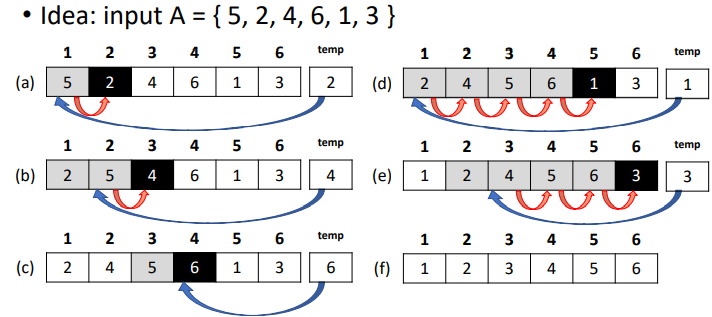public static void InsertSort(int arr[1]) { int insertVal=0; int insertIndex=0; for(int i=1;i<arr.length;i++) { //定义待插入的数 insertVal=arr[i]; insertIndex=i-1;//前一个数的下标 // 给 insertVal 找到插入的位置 // 说明 //1.insertIndex>=0 保证在给 insertVal 找插入位置，不越界 //2.insertVal<arr[insertIndex] 待插入的数，还没有找到插入位置 //3. 就需要将 arr[insertIndex] 后移 while(insertIndex>=0&&insertVal<arr[insertIndex]) { arr[insertIndex+1]=arr[insertIndex]; insertIndex--; } // 当退出 while 循环时，说明插入的位置找到,insertIndex+1 //这里我们判断是否需要赋值 if(insertIndex+1!=i) { arr[insertIndex+1]=insertVal; } }

4，Quick sort

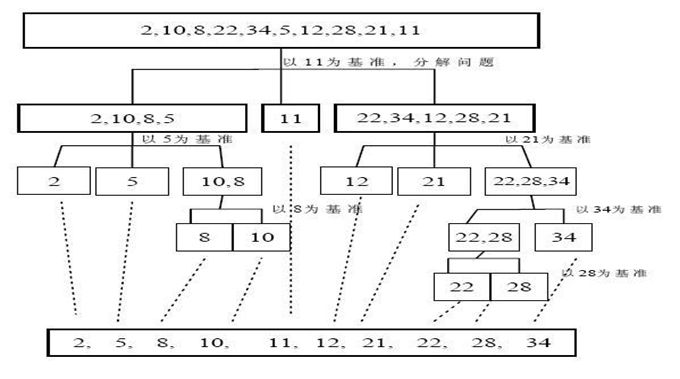 public static void QuickSortDemo(int []arr,int left,int right) { int l=left;//左下标 int r=right;//右下标 int temp=0; int pivot=arr[(left+right)/2];//选取它，其他数和它比较分类 //while 循环的目的是让比 pivot 值小放到左边 ，比 pivot 值大放到右边 while(l<r) { //在 pivot 的左边一直找,找到大于等于 pivot 值,才退出 while(arr[l]<pivot) { l+=1; } //在 pivot 的右边一直找,找到大于等于 pivot 值,才退出 while(arr[r]>pivot) { r-=1; } //如果 l>=r 说明 pivot 的左右两的值，已经按照左边全部是 //小于等于 pivot 值，右边全部是大于等于 pivot 值 if(l>=r) { break; } //交换 temp=arr[l]; arr[l]=arr[r]; arr[r]=temp; //如果交换完后，发现这个 arr[l]==pivot 值 相等 r--， 前移 //可以理解为：指定的pivot，里面有一个数和它相等，假如左边卡住，无法移动，右边退一步来推动查询 if(arr[l]==pivot) { r-=1; } //如果交换完后，发现这个 arr[r]==pivot 值 相等 l++， 后移 if(arr[r]==pivot) { l+=1; } } // 如果 l==r, 必须 l++,r--, 否则为出现栈溢出 if(l==r) { l+=1; r-=1; } if(left<r) { QuickSortDemo(arr,left,r); } if(right>l) { QuickSortDemo(arr, l, right); } }

5，Merge sort[no code] Divide and Conquer Approach

Stable/unstable	A stable sorting algorithm is any sorting algorithm that preserves the relative ordering of items with equal values.
In-place / Out-place	an in-place algorithm is an algorithm which transforms input using no auxiliary data structure.

总结

	

Non-comparison 1,counting sort(类似桶排序)

	 

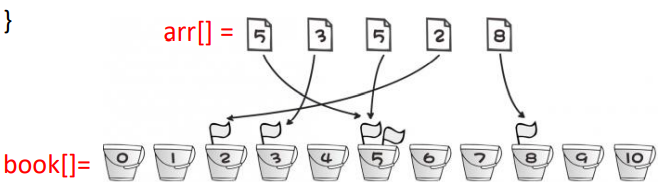2，bucket sort【stable】

	

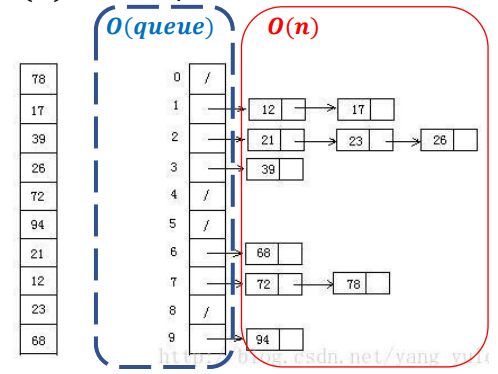3，Radix Sort【从右到左】
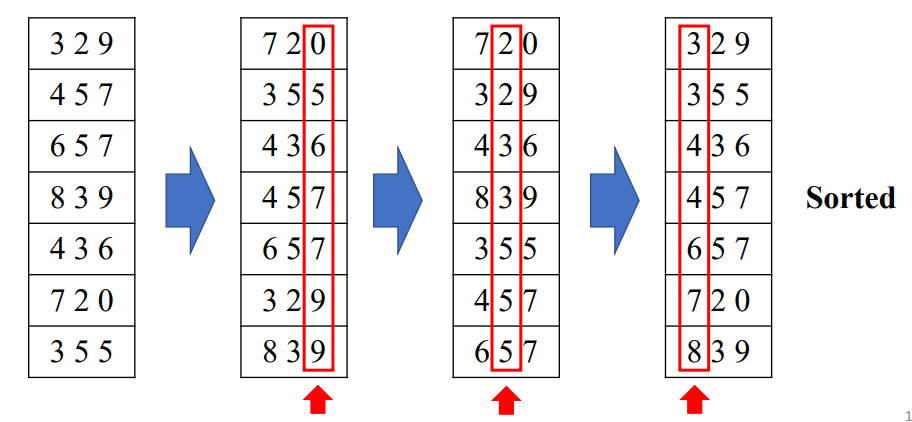