7 – Stacks and Queues

一、stacks 1，stack，先进后出 The stack mechanism is known as Last-In-First-Out (LIFO) because the last item inserted is the first one removed 【栈的解释】

2，操作 • There are several things you can do with a stack • Pop ( ) – pop the top item off the stack • Push ( ) – put another item onto the top • Peek ( ) – look at the top item and copy it

push ( element ) • insert an element at the top of the stack	
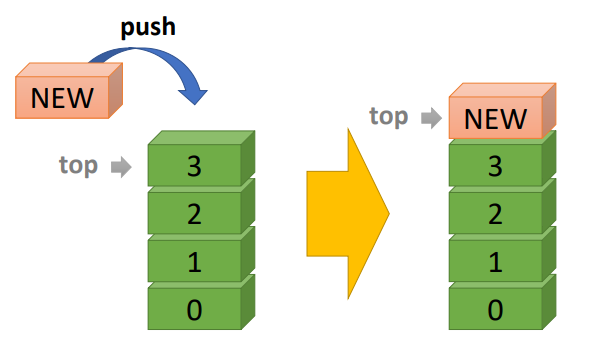• pop ( ) • remove an element from the top of the stack	
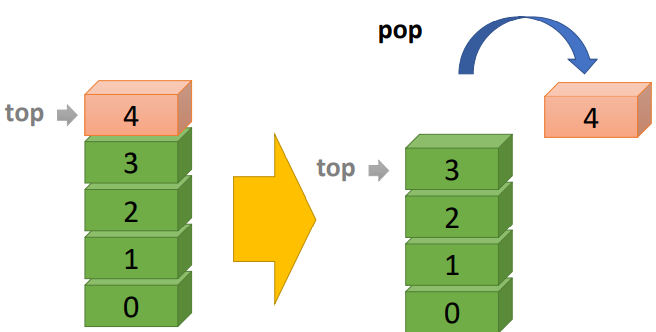• Peek ( ) • look at the top item and copy it	

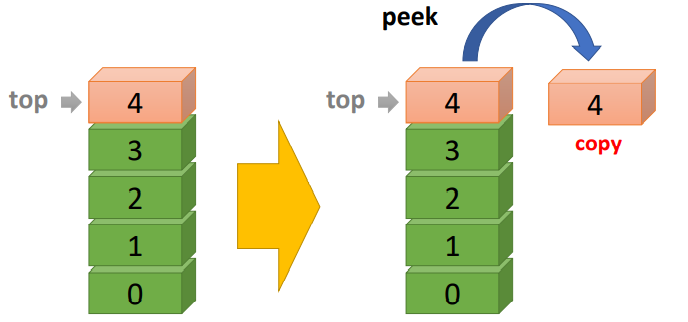其他操作 | • MakeEmpty( ) | Remove all items from the stack | |----------------|-----------------------------------------| | • IsEmpty( ) | True if stack is empty, false otherwise | | • IsFull( ) | True if stack is full, false otherwise |

3，用数组模拟stack Array-based Stack

初始情况：top=-1

1，stack满则A push operation will then throw a FullStackException • Limitation of the array-based implementation

• Not intrinsic to the Stack ADT 2，所需字段： maxSize，stackArray，top=-1

	  		

3, Can you think of anything else using a stack structure? • Web browsers • Undo sequence in a text editor • Java Virtual Machine

4，Method Stack in the JVM

6，例子 （1）The LIFO principle can be used in reversing a word （2）Checking for palindromes

7，Performance • Let 𝒏 be the number of elements in the stack • The space used is 𝑶(𝒏) • Each operation runs in time 𝑶(𝟏) (e.g. pop, push)

8,Limitations for array-based stacks • The maximum size of the stack must be defined a priori and cannot be changed 栈的长度已经定型 • Trying to push a new element into a full stack causes an implementation-specific exception 向满栈加入元素有异常

二、Queues 1,queues的解释： • A queue means to line up for something Queues uses the First-In-First-Out system (FIFO)， the one that has been in the queue the longest is the one that is popped

2,variables • Size of the array • The array itself • Variables for tracking front and rear

Empty Queue:	Front = 0, Rear = -1
3 items in queue:	Front = 0, Rear = 2

3，操作：加在rear，取走在front Insertions are made at one end, the back of the queue Deletions take place at the other end, the front of the queue

Front=0；rear=-1；

Insert	• Assumes the queue is not full • Inserts at rear • If rear is at the top of the array then it wraps around to the bottom of the array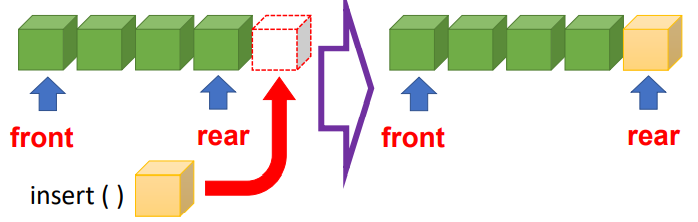 
Remove()	Assumes queue is not empty • Obtains the value at the front • Increments the front variable • If front goes beyond the end of the array it must be wrapped around to 0•如果front超过数组的末尾，它必须绕成0
peek ( )	Returns the value at the front
size ( )	Assumes queue not empty • Returns total number in queue
isFull ( )	• Returns true if queue is full
isEmpty ( )	• Returns true if queue is empty

案例

wrapround包着的 (rear+1)%maxSize==front [满]

4，Array-based Queue 代码

			 

案例 | Operation | Output | front ç Q ç rear | |---------------|------------|-----------------------| | insert(5) | - | 5 | | insert(3) | - | 5,3 | | remove() | 5 | 3 | | insert(7) | - | 3,7 | | remove() | 3 | 7 | | front() | 7 | 7 | | remove() | 7 | | | remove() | error | | | isEmpty() | true | | | insert(9) | - | 9 | | insert(7) | - | 9,7 | | size() | 2 | 9,7 | | insert(3) | - | 9,7,3 | | insert(5) | - | 9,7,3,5 | | remove() | 9 | 735 |

5，Performance • Let 𝒏 be the number of elements in the queue • The space used is 𝑶(𝒏) • Each operation runs in time 𝑶(𝟏)

6，• Limitations for array-based queues • The maximum size of the queue must be defined a priori and cannot be changed • Trying to insert a new element into a full queue causes an implementation-specific exception

三、Deque 1,• A deque is a double-ended queue 双端队列；双队列 insert items at either end and delete them at either end no longer a front and rear, simply two ends

2,操作

• insertLeft( )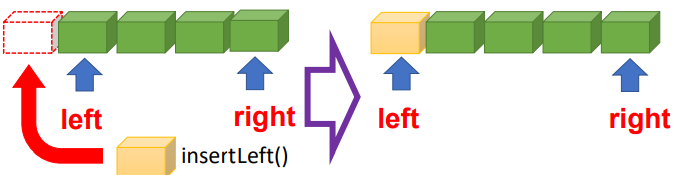	
• insertRight( )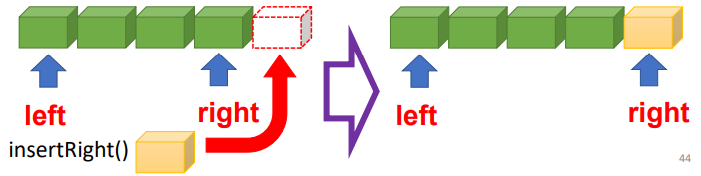	
• removeLeft( )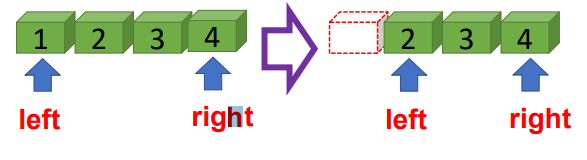	
• removeRight( )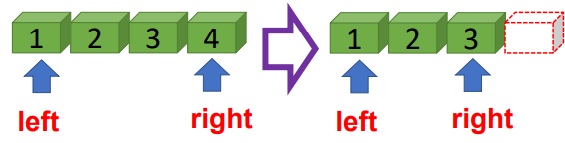	

3，

• A stack is actually a deque with only the methods • insertRight( ) • removeRight( )	
• A queue is a deque with only the methods • insertRight( ) • removeLeft( )	

四、Priority Queue 1，A priority queue is a queue where items don’t just join at the rear, they are slotted into the queue according to their priority 其中的项目不只是在后面加入，而是根据它们的优先级插入队列 2，操作 不需要front和rear，总是停留在索引0 only need to track the top

• Insert method has a for loop that shifts elements up 【shift elements up to make space rather 】

• Remove method simply removes the top (highest priority) element

是queue结构，但是类似栈，把最优先的放在“栈里的top”

	假设越小的数权重越大