7x-Heap Sort

叶子结点 就是出度为0的结点 就是没有子结点的结点 近二叉树：不能满的二叉树 一、binary tree 1，binary tree

2，Complete Binary Tree 定义：完备二叉树是指除了最后一层之外的每一层都是满的，并且所有节点都在尽可能远的左边的二叉树

堆：完全二叉树+父节点>子节点（父节点\<子节点） | max heap | 父>子 | |----------|--------| | Min heap | 父\<子 | . The heap can be represented by a binary tree or array.

3，Heap Property 3.1 a nearly complete binary tree with “heap property”:父节点>两个子节点 注意序号 3.2 从一开始

4，Tree height：从下往上； depth：从上往下

5，binary tree facts











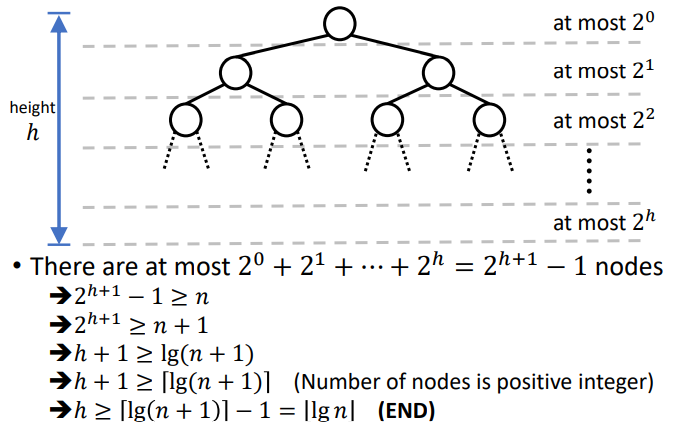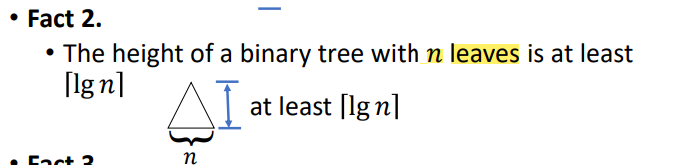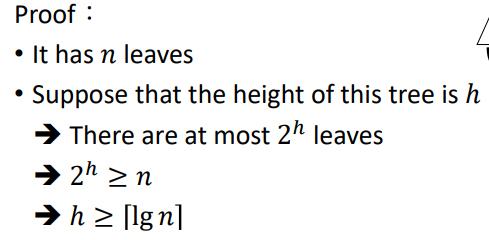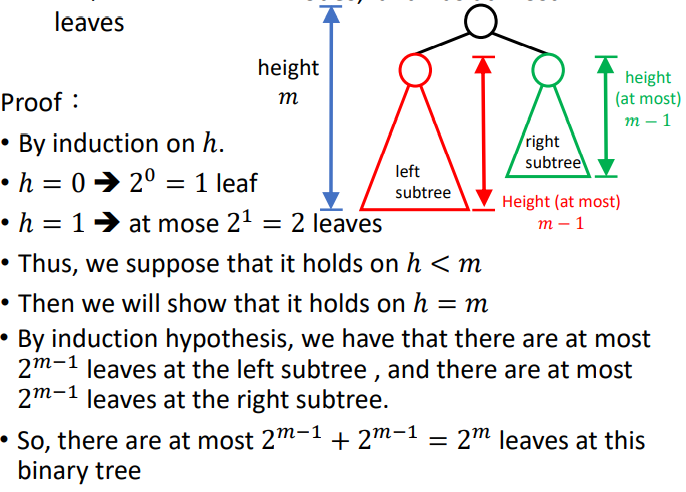数学公式

二、Heap Sort
1，

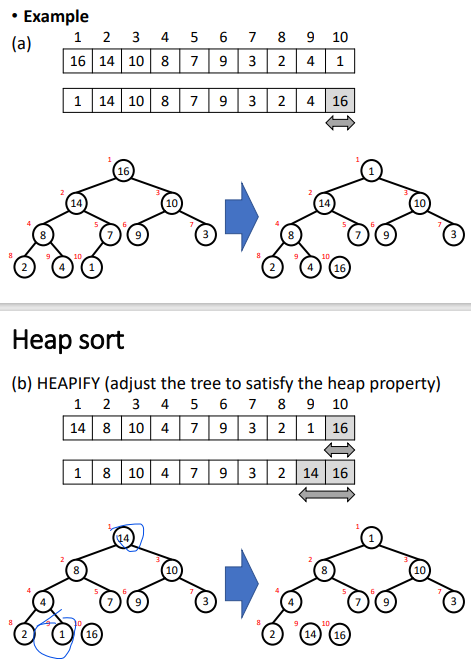
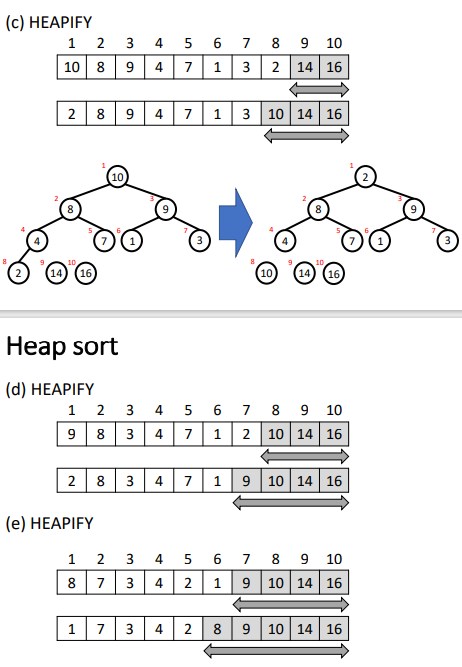
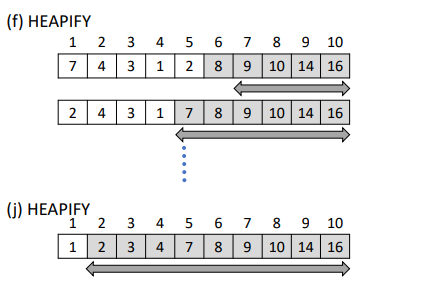
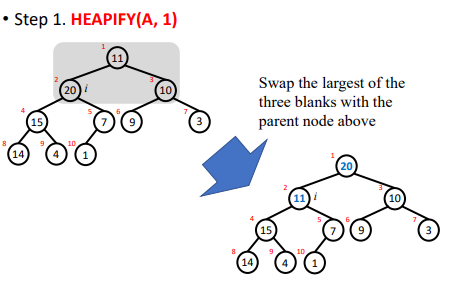
2，HEAPIFY[调整为heap tree]

		

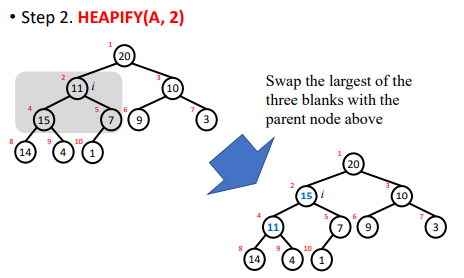
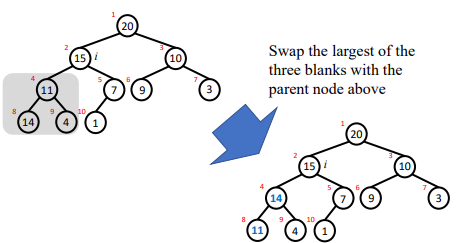
步骤 A is a heap 1，把A中最大的放到B 2，把最小的放到A[1] 3，调整剩余的node，【除了当前最大的】，直到满足heap 性质 4，重复1-3步直到A空 5，B就是从大到小排列好的数组

3，两个缺点 1，need a lot of extra space=O(1)

2,移动元素后的tree很可能不满足堆性质

4，heapify例子

		

5，时间复杂度

	

6，construct a heap tree 方法1：top-down O(nlgn) Extend the heap tree by add nodes one by one 从上至下,从左到右，一边加点一边调整结构 Then we add A[X] to this tree and do "floating up"

方法2：bottom up O(n) 从下往上，从右到左，开始构建 Use bottom up to construct heap ➔ 𝑂(𝑛)

时间复杂度：

7，堆排序时间复杂度

三、Priority queue