6.4.1最小生成树
1，概念¶
连通图的生成树是包含图中全部顶点的一个极小连通子图。【边尽可能的少，但要保持连通】
若图中顶点数为n，则它的生成树含有 n-1 条边。对生成树而言，若砍去它的一条边，则会变成非连通
图，若加上一条边则会形成一个回路。
2，树¶
3，最小生成树¶
案例
找出最便宜的修路方案
对于⼀个带权连通⽆向图G = (V, E)，⽣成树不同，每棵树的权（即树中所有边上的权值 之和）也可能不同。设R为G的所有⽣成树的集合，若T为R中边的权值之和最⼩的⽣成 树，则T称为G的最⼩⽣成树（Minimum-Spanning-Tree, MST）。
最⼩⽣成树可能有多个，但边的权值之和总是唯⼀且最⼩的 最⼩⽣成树的边数 = 顶点数 - 1。砍掉⼀条则不连通，增加⼀条边则会出现回路 |
|---|
一、Prim 算法（普⾥姆）：¶
从某⼀个顶点开始构建⽣成树； 每次将代价最⼩的新顶点纳⼊⽣成树，直到所有顶点都纳⼊为⽌。 从学校开始
不同的点出发，不同的分支选择，最小代价都一样
二、Kruskal 算法（克鲁斯卡尔）¶
每次选择⼀条权值最⼩的边，使这条边的两头连通（原本已经连通的就不选）直到所有结点都连通
| 最小1，两头未通 |  |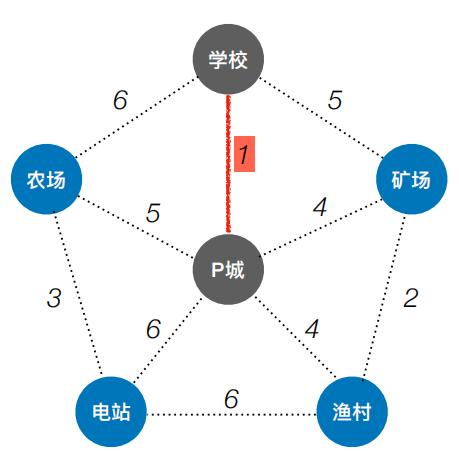
|---|---|
| 最小2，两头未通 |  |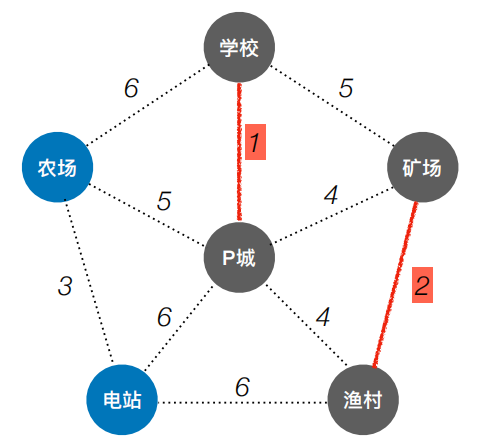
| 最小3，两头未通 |  |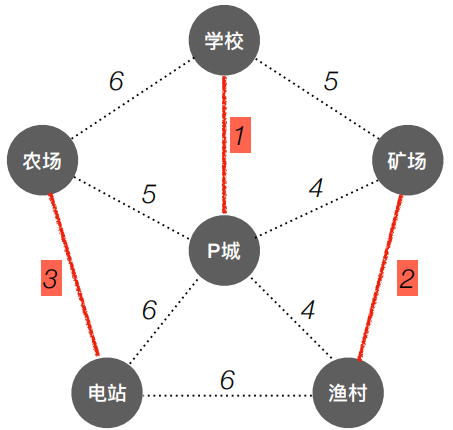
| 最小4，两头未通 |  |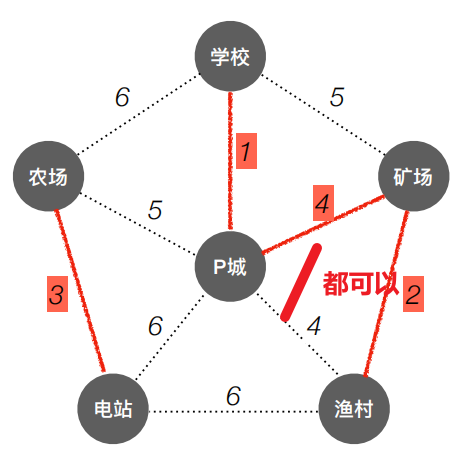
| 最小5，，两头未通 |  |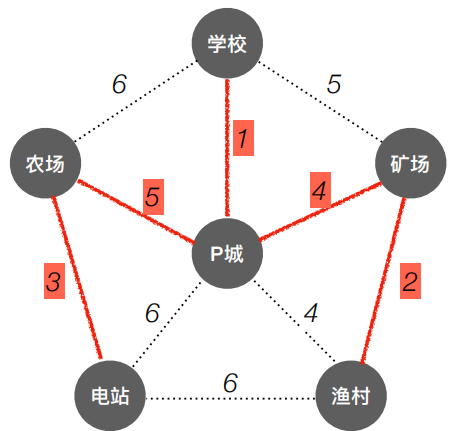
| 全部走通 |  |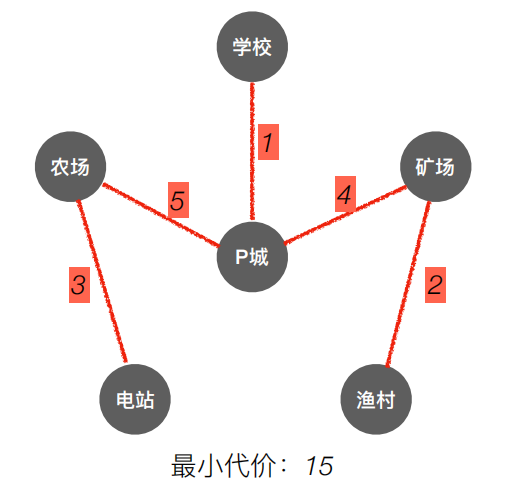
三、对比
四、实现思想 见PDF
