13-avl

为了解决：我们观察到，BST的最坏情况下的性能最接近线性搜索算法，即Ο(n)的问题而产生AVL

一、AVL Tree

1，Balanced Binary Tree 具有n个节点的二元搜索树的缺点是，它的高度可以高达n-1。

2，AVL 1）概念 平衡二叉树AVL=平衡二叉树+（平衡因子\<=1） AVL树是带有==平衡条件==的==二叉查找树== 特点：任意结点的平衡因子的绝对值不超过1 平衡因子=左子树高度-右子树高度 BF =height(left subtree) – height(right subtree) 案例 案例 目的

利弊

• Pros and Cons of AVL Trees 1. 搜索，插入和删除是O(log n)。 2. 高度平衡增加不超过一个恒定因素的插入速度。 1. Search, insertion and deletions are O(log n). 2. The height balancing adds no more than a constant factor to the speed of insertion. • Arguments against using AVL trees: 1. 难以编程和调试; 需要更多的空间来平衡因子。 2. 渐近更快，但再平衡需要时间。 3.大多数大型搜索是在磁盘上的数据库系统中完成的，并使用其他结构(例如b -树)。 4. 如果多个连续操作的总运行时间很快(例如展开树)，那么单个操作的运行时间为O(N)是可以的。 1. Difficult to program and debug; need more space for balance factor. 2. Asymptotically faster but rebalancing costs time. 3. Most large searches are done in database systems on disk and useother structures (e.g. B-trees). 4. May be OK to have O(N) for a single operation if total run time for many consecutive operations is fast (e.g. Splay trees).

二、Rotation

插入node 如果==左右子树的高度差大于1==，则使用一些==旋转技术对树进行平衡==。 为了平衡自身，AVL树可以执行以下四种旋转−

1，Left rotation

LL平衡旋转（右单旋转） 原因：在结点A的左孩子的左子树上插入新结点 调整方法：右旋操作：将A的左孩子B代替A，将A结点称为B的右子树的根节点，而B的原右子树作为A的左子树【把B拎起来，A下去，B的右子树称为A的左子树】 案例

2， Right rotation

RR平衡旋转（左单旋转） 原因：在结点A的右孩子的右子树上插入了新结点 调整方法：左旋操作：将A的右孩子B代替A，将A结点称为B的左子树根节点，而B的原左子树作为A的右子树【把B拎起来，A左边放下去，把B的左子树给A的右子树】

如何定位A,B? A就是==距离插入点最近==，且==平衡因子不平衡==的那个点

案例

不，要LR选择

3，Left-Right rotation

LR平衡旋转（先左后右双旋转）【先对B左旋，C领上来，再对C右旋】 原因：在结点A的左孩子的右子树上插入新的节点 调整方法：先左旋转在右旋转：将A的左孩子B的右孩子C代替B，再将C向上代替A

案例

4，Right-Left rotation

RL平衡旋转（先右后左双旋转） 原因：在结点A的右孩子的左子树上插入了新结点【对B右旋转，把C提上来，再对C左旋转，把C上来】 调整方法：先右旋转再左旋转，将A的右孩子B的左孩子结点C代替B，再将C结点上调至A的位置

三、在操作时，调整平衡因子

1，插入

• Insert 新节点总是作为叶节点插入，平衡因子等于0。

插入步骤 1，转到相应的叶节点，以使用以下递归步骤插入新节点。比较当前树的newKey和当前树的rootKey。 1）如果newKey\<rootKey，在当前节点左子树上调用插入算法，直到到达叶节点。 2）否则，如果是newKey>根键，则在当前节点的右子树上调用插 入算法，直到到达叶节点。 3）Else, return leafNode 4）更新平衡因子，做调整

2，删除

• Delete ==先按照BST要求删除节点，在调整平衡因子== 一个节点始终作为一个叶节点被删除。删除节点后，节点的平衡系数会发生更改。为了重新平衡平衡因子，我们进行了适当的旋转。

三种情况 1，如果没有删除是叶节点。没有任何子级)，然后删除未删除。 2，如果未删除有一个子项，则将未删除的内容替换为子项的内容。删除该子项。 3，如果没有被删除的人有两个子级，请找到没有被删除的人的顺序继承者w。在右侧子树中具有最小键值的节点）。 用未删除的内容替换为w的内容。

删除叶子节点w

4，更新节点的平衡系数。

5，

• Max and Min 1，最小--》最左边

• Complexities of Different Operations【重点】

四、计算高度和点数

一个高度为h的AVL | 最少放 | | |--------|-------------------------------------------------------------------------------------------------------------------------| | 最多放 | | 补充斐波那契数列 案例

最少放	F5-1=5-1=4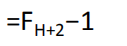 
最多放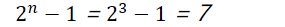	

案例 | 高度是4的avl数，有可能放50个点吗 | |-------------------------------------------------------------------------------------------------------------------------| | |

补充： 高度为h的最小平衡二叉树的结点数Nh (最小--》结点最少)

分析过程 - 为什么左子树Nh-1?--->保证树的高度为h - 右子树分析