16-图-拓扑排序
¶
• Topological Sorting¶
==== 1，概述 拓扑排序主要用于从作业之间的给定依赖关系中调度作业【==找到做事情的顺序==】
有向无环图的拓扑排序(DAG)是顶点的线性排序，对于每一条有向边uv，顶点u在顺序在v之前。
如果图不是DAG，则不能对图进行拓扑排序。 拓扑排序当且仅当图是一==个有向无环图时==才可以排序。
2，有向图 有向图可以用来表示一组事件中的优先级
fact： 如果G包含一个循环，则无法找到所需的顺序•（通过矛盾来证明） 然而，如果G是无环的（不包含循环），我们将给出两种算法，它们总是能找到所需的排序 案例
有向无环图directed acyclic graph.
寻找拓扑排序数量 | 1，写入每个顶点的入度，删除当前入度最小的点，更新各点入度 | |-----------------------------------------------------------|
Problem01
找到给定图可能的不同拓扑顺序的数量
上图的拓扑顺序的步骤如下。
案例2
考虑一下下面给出的有向图。以下哪些说法为真
1.该图没有任何拓扑顺序。【错，】
2.PQRS和SRPQ都是拓扑顺序。【】
3.PSRQ和SPRQ都是拓扑顺序。
4.PSRQ是唯一的拓扑顺序。
解决：3正确
1，给定的图是一个有向无环图。因此，拓扑顺序的存在。
2，根据拓扑排序的定义，P和S必须以拓扑顺序出现在R和Q之前。
案例3
请考虑下面的有向图。
先删去A，有B,D两种情况，
从B入手，删B，有C,D两种情况，删C，得到==结果1==，删D，有C,E两种情况，得到结果2,结果3
从D入手，删D，有B,E两种情况，删E，得到结果4，删B，有C,E两种情况，得到结果5,结果6
我们介绍了有向无环图(DAG)上的拓扑排序问题
我们给出了两种线性时间算法： • (1) Using Queue • (2) Using Stack
1，Using Queue Example of Topological Sort (with Queue) 思路：存入度=0的
Example of Topological Sort - 2
4，Topological Sort (with Queue)
Topological Sort (Example)
二、Topological Sort (with Stack)
1，Topological Sort (with Stack)
1.在图上使用==DFS==
2.按顶点结束时间的递减顺序排列的输出顶点；==（其完成时间的递减顺序==）
2，
• (check time, finishing time)
Topological Sort (with Stack)
Topological Sort (Example)
在可能的DFS后的发现和完成时间
时间完成时间（按降序排列） 如果我们从左到右排序事件，边缘方向有什么特别之处吗？
Performance 设G=（V、E）为输入有向图 拓扑排序的运行时间： 1.执行DFS：O(|V|+|E|)时间
2.排序完成时间
Total time: O(|V|+|E|)
案例
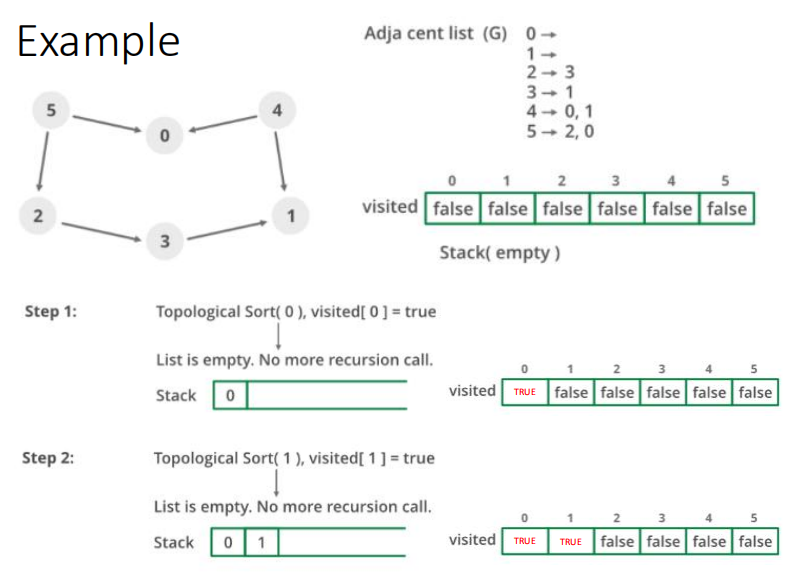
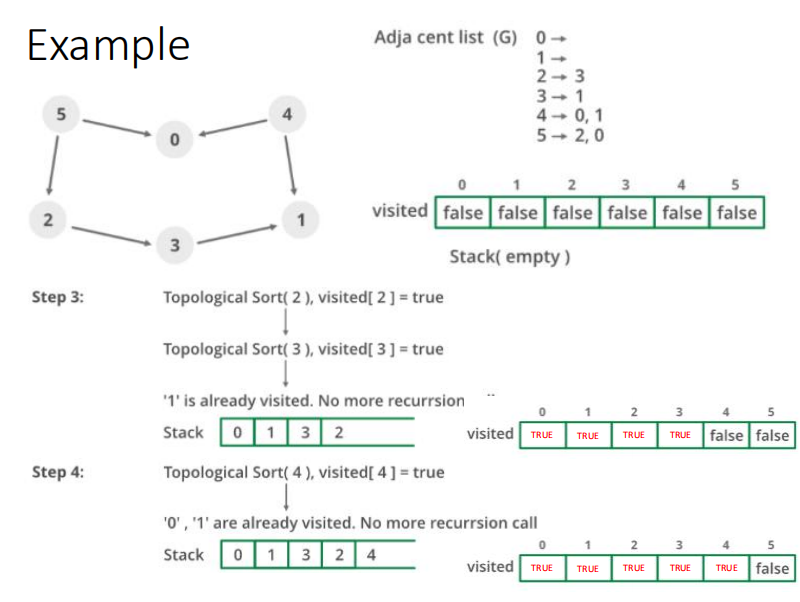
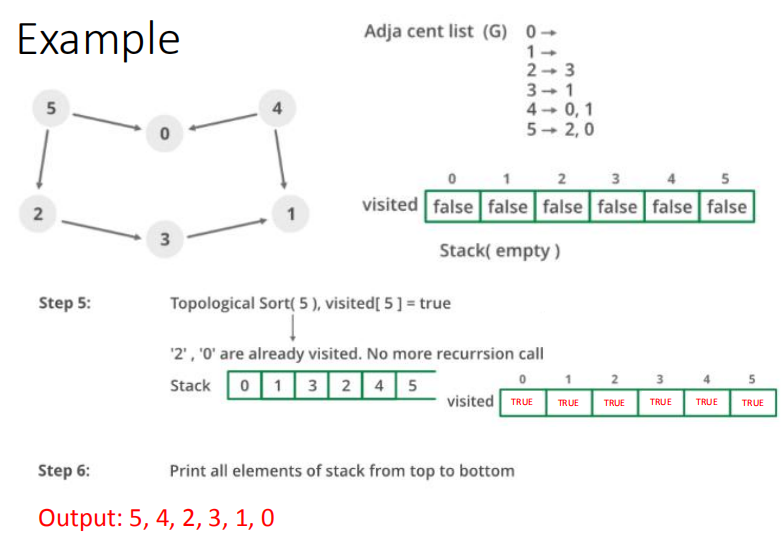
然后我们按节点顺序遍历这个图 0-5这个顺序 首先dfs的是0这个点 dfs进去发现他没有子节点 也就是没有从0这个点出发可以到达的点 然后把0添加到栈里面 然后dfs的是1这个点 1这个点和0同理，没有子节点，然后把1添加到栈里面 然后遍历2 2有一个子节点3 所以我们先把visit2设为true，然后dfs 3这个节点 visit代表这个点已经访问过了 3到1 但是1已经访问过了，所以结束当前的dfs 同时把3放进栈里面 再把2放进栈里 这样我们栈里面，就是 0 1 3 2 0在栈底 这样2这个节点就算是深搜完了 然后深搜3 但是3已经访问过了，直接跳过 然后4，发现4的两个子节点0和1也已经访问过了 然后栈是后进先出的原理 倒过来正好就是拓扑的顺序 |
|---|
   |
|---|
